[정렬알고리즘] 5개 정렬 알고리즘 비교

 

대표적인 5가지 정렬 알고리즘을 직접 구현하고, 데이터 크기에 따른 성능을 비교하고 분석. 
알고리즘의 동작에 대한 분석 및 구현 코드의 설명.

2022.11.14 - [Algorithm] - [정렬알고리즘] Selection Sort 선택 정렬

[정렬알고리즘] Selection Sort 선택 정렬

2022.11.14 - [Algorithm] - [정렬알고리즘] Median of Three Quick Sort 중간 값 분할 빠른 정렬

[정렬알고리즘] Median of Three Quick Sort 중간 값 분할 빠른 정렬

2022.11.14 - [Algorithm] - [정렬알고리즘] Shell Sort 쉘 정렬

[정렬알고리즘] Shell Sort 쉘 정렬

2022.11.14 - [Algorithm] - [정렬알고리즘] Bitonic Sort 바이토닉 정렬

[정렬알고리즘] Bitonic Sort 바이토닉 정렬

2022.11.14 - [Algorithm] - [정렬알고리즘] Odd Even Merge Sort 홀짝합병정렬

[정렬알고리즘] Odd Even Merge Sort 홀짝합병정렬

 

---

Implementation

main

데이터 크기는 n,  n의 데이터 크기를 갖는 배열의 원소들범위는 0부터 n*10까지 로 임의로 설정하였다. 

각 알고리즘에 들어가는 데이터를 동일하게 하여 알고리즘 간 성능 비교를 하기 위해 각 배열들을 동적 배열로 선언하고, System Time을 이용하여 Random Variable을 발생시켜 random한 데이터 셋을 저장하였다. 이 배열을 알고리즘에 들어가는 각자의 배열로 copy()함수를 이용하여 복사하였다. copy() 함수를 사용하기 위해 Algorithm 라이브러리를 추가시켰다. 복사한 배열을 각각의 정렬 알고리즘에 원소로 넣고, 실행시간을 측정하였다. 

동적으로 배열을 선언했기 때문에 꼭 delete 로 할당한 메모리를 없애 줘야한다. 

int main(void){
	int n = 16; //배열에 저장될 원소 갯수 2의 지수승, 임의로 128, 512, 1024, 4096, 16384, 65536, 262144, 524288, 1048576
	int range = n*10;//원소값의 범위. (임의 설정).
	int *arr1, *arr2, *arr3, *arr4, *arr5;//각 알고리즘 별 실행할 배열 5개. 
	arr1 = new int[n]; arr2 = new int[n]; arr3 = new int[n]; arr4 = new int[n]; arr5 = new int[n]; 

	srand((unsigned int)time(NULL));
	for(int i=0; i<n; i++){
		arr1[i] = rand() % range;//0~range-1까지 random 난수 생성. 
	}
	copy(arr1, arr1+n, arr2);copy(arr1, arr1+n, arr3); copy(arr1, arr1+n, arr4); copy(arr1, arr1+n, arr5);

	ShowArray(arr1, n); //정렬되기 전 데이터 확인. 

	Selection(arr1, n, range); //Selection Sort
	ShowArray(arr1, n); 
	delete[] arr1;

	MoTQuick(arr2, n); //Median of Three Quick Sort
	ShowArray(arr2, n); 
	delete[] arr2;

	Shell(arr3, n); //Shell Sort
	ShowArray(arr3, n); 
	delete[] arr3;

	Bitonic(arr4, n); //Bitonic Sort
	ShowArray(arr4, n); 
	delete[] arr4;

	OddEvenMerge(arr5, n); //Odd Even Merge Sort
	ShowArray(arr5, n); 
	delete[] arr5;

	return 0;
}

void ShowArray(int* arr, int n){
	for(int i=0; i<n; i++){
		cout<<arr[i]<<' ';
	}
	cout<<endl<<endl;
}

 

Result

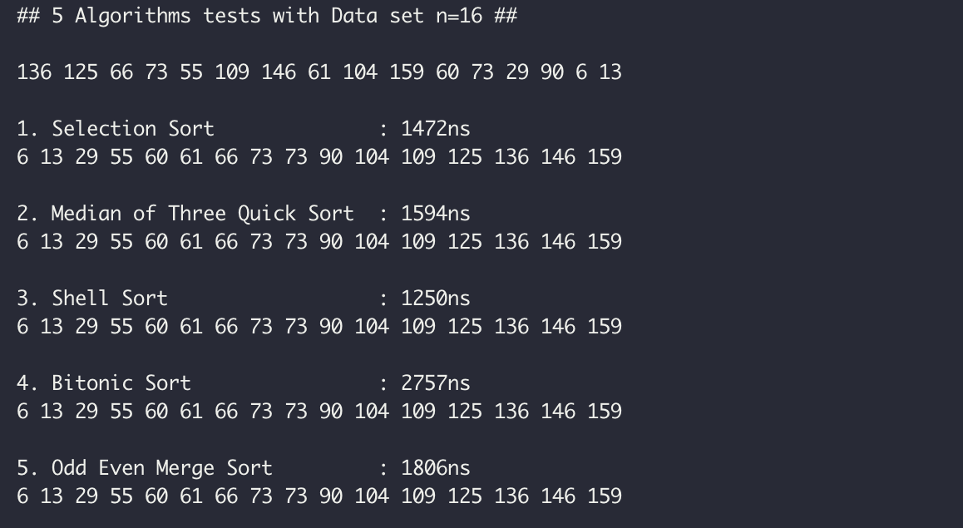
데이터 수가 2^4 = 16 일 때, 정렬이 올바르게 되는지 확인과 소모 시간.

 

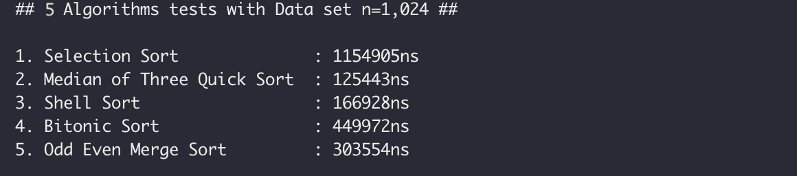
데이터 수가 2^10 = 1024

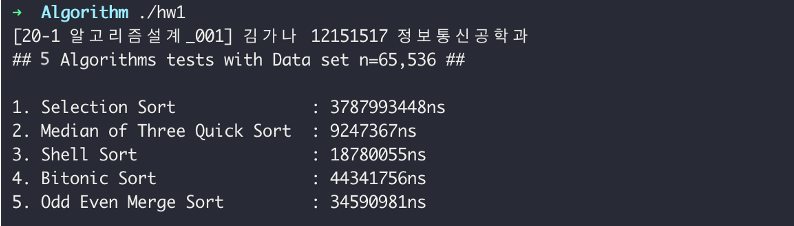
데이터 수가 2^16 = 65,536

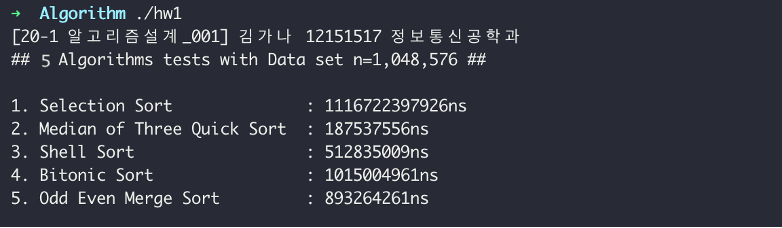
데이터 수가 2^20 = 1,048,576 

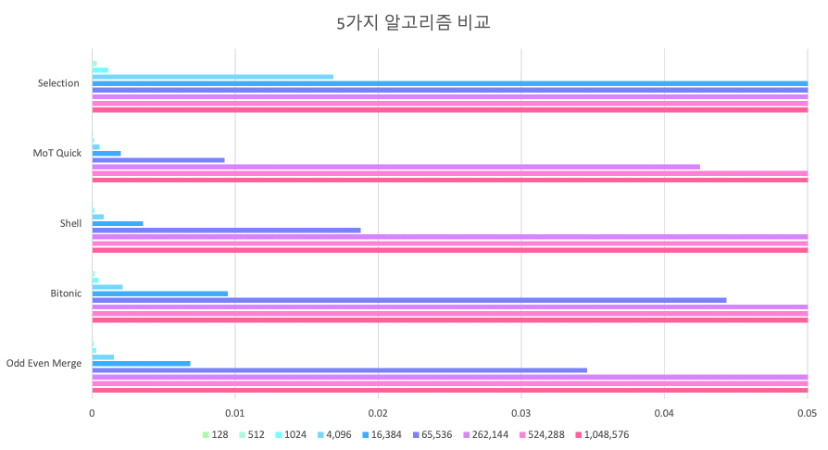
Conclusion

100개 정도의 작은 데이터에서의 실행시간을 분석해봤을 때 5개의 알고리즘 모두 매우 작은 시간이 걸렸다. 즉 정말 작은 데이터를 정렬하는 데는 어떠한 알고리즘을 써도 빠른 시간 안에 결과값을 얻을 수 있다. 하지만 이러한 상황에서도 정렬된 데이터가 들어오면 O(n^2) 의 시간이 걸리게 되므로 주의해야한다. 

데이터를 2^n 개로 늘려가며 정렬을 수행하였을 때, 중간 값 분할 빠른 정렬이 성능이 가장 좋았고, 선택 정렬이 가장 나빴다. 

데이터 500개부터는 Selection Sort는 다른 정렬 알고리즘들 보다 10배 이상 오래 걸리므로 사용하지 않는 것이 좋을 것 같다. 또한 데이터 50,000개부터는 정렬 수행에1초 이상 걸리기 시작했다. 이는 선택 정렬 알고리즘은 원하는 값의 위치를 데이터 개수 – 1 번씩 비교하며 찾아가기 때문에 당연히 데이터 수가 많아지면 실행 시간이 길어지게 된다. 

그 다음으로 Bitonic Sort가 실행 시간이 오래 걸렸다. 하지만 Bitonic Sort 알고리즘은 병렬 프로세서에서 쓰이게 끔 만들어진 알고리즘이기 때문에 GPU에서 Sort 따로 Merge 따로 병렬 처리하여 실행시키면 오늘 나온 실행 결과보다 더 빠른 실행시간을 얻을 수 있을 것이다. 일반 CPU 에서는 Sort 함수로 데이터를 분할하고 Merge 함수로 데이터를 정렬하고 다시 재 병합하고, 또다시 분할하는 동작을 순서대로 처리하기 때문에 효율적인 알고리즘임에도 불구하고 처리 속도가 오래 걸렸다. 특히 Bitonic Sort는 100만개가 넘어가는 데이터 정렬부터는 1초이상 걸렸다. GPU 에서의 테스트가 필요해 보인다.

그 다음은 Odd Even Merge Sort이다. Bitonic Sort 알고리즘과 마찬가지로 병렬 프로세스에서 쓰이게끔 만들어진 알고리즘이기 때문에 실행 시간이 오래 걸렸다. 하지만 Bitonic Sort 와는 달리 재정렬에 필요한 연산 수가 적기 때문에 Bitonic 보다는 항상 빨랐다. 병렬 프로세스를 이용해 알고리즘을 실행한다면 컴퓨터 메모리 크기를 넘지 않는 이상 가장 빠른 알고리즘이라고 한다. 

두번째로 좋았던 정렬 알고리즘을 Shell 정렬 알고리즘이다. 쉘 정렬은 100만개가 넘는 데이터 정렬 에도 0.5초 정도 실행 시간이 걸리는 것을 확인했다. Gap 값을 이용해서 멀리 떨어진 값 끼리 정렬을 수행하기 때문에 데이터 끝까지  

비교를 하지 않아도 된다. 

가장 좋았던 알고리즘은 중간 값 분할 빠른 정렬 알고리즘 이었다. 중간 값 분할은 첫 중간 끝 값 중 중앙값을 pivot값으로 이용하기 때문에 적절하게 pivot 을 중심으로 데이터가 나눠지고 정렬이 수행된다. 이러한 수행 과정때문에 100만개 이상의 데이터를 정렬하는데도 0.2초 정도 밖에 걸리지 않았다. 

위와 같은 결과로 인해 내가 짠 정렬 알고리즘들을 실행 시간으로 비교해본 결과 

1. Median Of Three Quick Sort  2. Shell Sort  3. Odd Even Merge Sort  4. Bitonic Sort  5. Selection Sort

순으로 성능이 좋았다. 하지만 Bitonic Sort와 Odd Even Merge Sort 같은 경우에는 GPU 에서 실행을 해봐야지 더 정확한 결과를 얻을 수 있을 것 같다.

 

얻은 결과를 표로 나타내면, 아래와 같으며

	실행시간(n = 100만)	시간 복잡도	Stable	In-Place
MoT Quick	0.19초	O(nlogn)	No	Yes
Shell	0.51초	O(logn)	Yes	Yes
Odd Even Merge	0.89초	O(log^2(n))	No	Yes
Bitonic	1.02초	O(log^2(n))	No	Yes
Selection	1116.72초	O(n^2)	No	Yes

안정성과 추가 저장공간에 대한 것까지 따졌을 때는 Shell Sort 알고리즘이 가장 좋을 것 같다.