[정렬알고리즘] Odd Even Merge Sort 홀짝합병정렬

대표적인 5가지 정렬 알고리즘을 직접 구현하고, 데이터 크기에 따른 성능을 비교하고 분석. 
알고리즘의 동작에 대한 분석 및 구현 코드의 설명.

Odd Even Merge Sort _ 홀짝 합병 정렬

시퀀스를 계속 반으로 분리하고 다시 merge 하는 정렬. 

홀짝 합병 정렬 알고리즘은 병렬 프로세서에서 구현에 적합하게 만들어진 알고리즘이다. Bitonic Sort 와 마찬가지로 Merge Sort를 기본으로 하지만, Bitonic Sort 와 달리 오름차순, 내림차순의 bool 값이 들어가지 않고, 현재 원소 로부터 다음 원소까지 떨어진 거리에 대한 값이 들어간다. 이 값을 이용해 짝수 인덱스들끼리, 홀수 인덱스들 끼리 정렬을 한 후에 Merge 함수로 합한다. 또한 정렬 된 값을 저장하기 위한 새로운 저장공간이 필요하지않다.

홀짝 합병 정렬 알고리즘을 반으로 계속 나누어 정렬 하다 보면 0으로 시작하여 1로 끝나는(오름 차순), 혹은 1로 시작하여 0 으로 끝나는(내림차순) 0-1 Sequence 형태로 나타나게 된다. 

Bitonic Sort와 같은 값으로 직접 표현해 보았다.

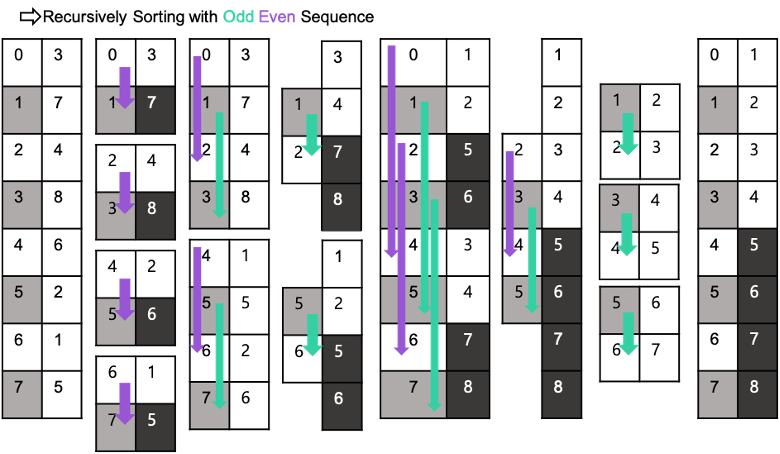
위의 예제에서 알 수 있듯이 Bitonic Sort 와 비슷한 듯 다르다. 계속 반으로 나눠지고 다시 합쳐지는 Merge 함수 과정에서 0-1 Sequence 모양이 나타나는 것도 알 수 있다. 

또한 Bitonic Sort와 비교하였을 때 재정렬에 소모되는 연산 횟수가 적어졌다. 

Parallel time 에서의 시간 복잡도는 최선의 경우 O(log^2(n)) , 평균은 𝜃(log^2(n)) , 최악의 경우에는  O(nlog^2(n))이 나온다. 

Bitonic Sort와 마찬가지로 새로운 저장공간이 필요하지 않으므로 in-place 정렬이고, Odd-Even 순서에 따라 정렬되기 때문에 Unstable한 정렬이다. 

 

Implementation

Swap 함수

모든 정렬 알고리즘에서 Swap 모듈을 사용하므로, 함수화 하여 사용한다. 

동적 배열의 주소 값과 정수 값 두개를 인자로 받고 첫번째 인자 a 와 두번째 인자 b를 index 로 하는 배열의 두 값을 바꿔주는 함수이다. 

void Swap(int* arr, int a, int b){
	int temp = arr[a];
	arr[a] = arr[b];
	arr[b] = temp;
}

Odd Even Merge Sort

Odd Even Merge Sort 함수인자로는 start 와 데이터 크기를 받는다. 크기를 반으로 줄여가며 최소 2개짜리의 Sequence 로 계속 나누며 Odd Even Merge 함수를 통해 정렬하고 합치게 된다. 

Odd Even Merge 함수는 인자로 start, 데이터 크기, distance 값을 받는다. Distance 의 초기 값은 1이다. 거리 값에 2씩 곱하며 Comparator 비교기 함수로 정렬하고 합친다. 비교 할 거리가 데이터 크기 보다 커졌다면 거리만큼 떨어진 원소들과 비교하여 정렬 혹은 재정렬 한다. 이를 반복하다 보면 정렬이 start가 짝수 먼저, 그 다음은 start가 홀수인 순서로 정렬이 이뤄지게 된다. 이로 인해 재정렬에 필요한 비교 단계도 줄어들게 된다.

Comparator 비교기 함수는 오름 차수로 비교를 하여 두 원소의 알맞은 위치를 찾아준다.

 

class OddEvenMergeSorter{
public:
	void OddEvenMergeSort(int* arr, int start, int n){
		if(n>1){
			int k = n/2;
			//recursively sorts two seqeunce
			OddEvenMergeSort(arr, start, k); //0~n/2까지 시퀀스가 계속해서 반으로 나눠진다. 
			OddEvenMergeSort(arr, start+k, k); //n/2~n까지 시퀀스가 계속 반으로 나눠진다. 
			//^-- merges the two halves
			OddEvenMerge(arr, start, n, 1); //반으로 나눠진것들을 sorting 하며 다시 정합한다.  
			//^-- picks every "2*distance" th element starting fromt position start and start+distance
		} //여기까지는 bitonic sort와  동일하다.
	}
	void OddEvenMerge(int* arr, int start, int n, int distance){
		int k = distance*2; //odd even 이기 때문에 매번 starting point로부터 2*distance 번째 원소를 선택한다. 
		//계속 재귀호출 하면서 key값은 1,2,4,8 .. 식으로 늘어나게된다. 
		if(k<n){
			OddEvenMerge(arr, start, n, k); //even sequence (짝수부분)
			OddEvenMerge(arr, start+distance, n, k); //odd sequence (홀수부분)
			for(int i = start+distance; i+distance<start+n; i+=k) //그 다음 k거리 원소와 비교 
				Comparator(arr, i, i+distance); //start부터 거리만큼 떨어진 원소부터 거리차이만큼 나는 원소와 비교하여 정렬한다. 
		}else {//key 값이 데이터 크기 보다 커졌다면 
			Comparator(arr, start, start+distance); //재정렬
		}
	}
	void Comparator(int* arr, int i, int j){
		if(arr[i] > arr[j]) Swap(arr, i, j); //오름 차순 정렬이다. 
	}
};
void OddEvenMerge(int* arr, int n){ //Odd Even Merge Sort
	OddEvenMergeSorter oems;
	steady_clock::time_point start, end; nanoseconds result; 
	start = steady_clock::now();

	oems.OddEvenMergeSort(arr, 0, n);

	end = steady_clock::now(); result = end - start;
	cout<<"5. Odd Even Merge Sort         : "<<result.count()<<"ns"<<endl; //알고리즘 실행시간
}